11. Mass and Center of Mass

b. Center of Mass

This page is not calculus, but provides the background physics for the subsequent pages.

1. Discrete Masses

Consider a balance beam with several weights (here \(3\)) at various positions. Find the center of mass, \(\bar{x}\), which is the position for the pivot at which the weights are exactly balanced.

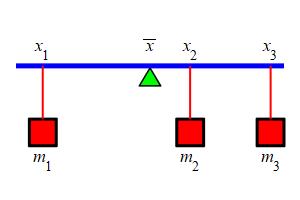
From physics we know that the balance condition is that the torques (the product of the weight and the lever arm) are exactly balanced. With \(3\) masses arranged as in the picture, this says \[ m_1g(\bar{x}-x_1)=m_2g(x_2-\bar{x})+m_3g(x_3-\bar{x}) \] Notice that the lever arms are all positive, since for the mass to the left of the pivot \(\bar{x}-x_1 \gt 0\) while for the masses to the right of the pivot \(x_2-\bar{x} \gt 0\) and \(x_3-\bar{x} \gt 0\). Also notice that we have assumed that there are two masses to the right of the pivot and one to the left. However, this is not important since we can rewrite the balance equation as \[ m_1g(\bar{x}-x_1)+m_2g(\bar{x}-x_2)+m_3g(\bar{x}-x_3)=0 \] so that there is no distinction between masses on the left and masses on the right. We wish to solve this equation for the position of the pivot, the center of mass \(\bar{x}\). So we cancel \(g\)'s, collect terms involving \(\bar{x}\) and take the remaining terms to the other side: \[ (m_1+m_2+m_3)\bar{x}=m_1x_1+m_2x_2+m_3x_3 \] So the center of mass is at: \[ \bar{x}=\dfrac{m_1x_1+m_2x_2+m_3x_3}{m_1+m_2+m_3} \] Notice that the same derivation would work for any number of masses, say \(n\), and the result would be: \[ \bar{x} =\dfrac{m_1x_1+m_2x_2+\cdots+m_nx_n}{m_1+m_2+\cdots+m_n} =\dfrac{\sum\limits_{i=1}^n m_ix_i}{\sum\limits_{i=1}^n m_i} \] where we have rewritten the result using summation notation. The denominator is just the total mass: \[ M=\sum_{i=1}^n m_i=m_1+m_2+\cdots+m_n \] The numerator is called the first moment of the mass: \[ M_1=\sum_{i=1}^n m_ix_i=m_1x_1+m_2x_2+\cdots+m_nx_n \] In terms of these, the center of mass is: \[ \bar{x}=\dfrac{M_1}{M} \]

When you hear the word first moment, you naturally ask: “What are the second and higher moments?”

The second moment of the mass is: \[ M_2=\sum_{i=1}^n m_ix_i^2 \] and similarly, the \(k^\text{th}\) moment of the mass is: \[ M_k=\sum_{i=1}^n m_ix_i^k \] These are used in various physical applications, for example, the second moment occurs in the formulas for moment of inertia on a later page

The center of mass of \(n\) masses \(m_1,m_2,\ldots m_n\) located at \(x_1,x_2,\ldots x_n\) respectively is: \[ \bar{x}=\dfrac{M_1}{M} \] where the total mass is: \[ M=\sum_{i=1}^n m_i \] and the first moment of the mass is: \[ M_1=\sum_{i=1}^n m_ix_i \]

Find the total mass and the center of mass of four masses whose masses and locations are

\(i=\)	\(1\)	\(2\)	\(3\)	\(4\)
\(m_i=\)	\(2\,\text{gm}\)	\(5\,\text{gm}\)	\(4\,\text{gm}\)	\(3\,\text{gm}\)
\(x_i=\)	\(-1\,\text{cm}\)	\(2\,\text{cm}\)	\(3\,\text{cm}\)	\(5\,\text{cm}\)

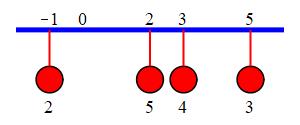
\(M=14\,\text{gm}\)
\(bar{x}=\dfrac{5}{2}=2.5\,\text{cm}\)

\[ M=\sum_{i=1}^4 m_i=2+5+4+3=14\,\text{gm} \] \[ M_1=\sum_{i=1}^4 m_ix_i =2\cdot(-1)+5\cdot2+4\cdot3+3\cdot5=35\,\text{gm-cm} \] \[ \bar{x}=\dfrac{M_1}{M} =\dfrac{35}{14}=\dfrac{5}{2}=2.5\,\text{cm} \]

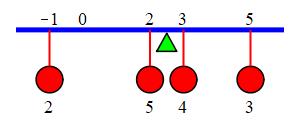
Notice that the center of mass at \(\bar x=2.5\) is within the range of the objects which stretch from \(x=-1\) to \(x=5\).

On the next page, we will find the center of mass of a bar for which the mass is not uniformly distributed.

11. Mass and Center of Mass

b. Center of Mass

1. Discrete Masses

Heading